Graphes et tas (2)

Les Tas

L’algorithme de Dijkstra est un algorithme de type glouton : à chaque nouvelle étape, il va "manger" un nouveau sommet. Le choix du sommet se fera en comparant les distances au sommet source. Or, une implémentation naïve ne permettra d’extraire le minimum d’un ensemble de sommets qu'en O(n) , si bien que l’algorithme de Dijkstra serait en O(n³) , ce qui est trop lent !

On peut mieux faire, et les tas sont justement une structure idéale pour cela.

Définition

On part donc d’un ensemble muni d’une relation d’ordre. L’idée de base est la suivante : toute recherche dans un arbre de taille n "correctement organisé" se fait en O(ln n) ; il ne reste donc plus qu'à organiser correctement notre arbre. Un tas est ainsi un arbre bien rempli, c'est-à-dire que tous ses niveaux sont remplis au maximum sauf éventuellement le dernier où toutes les feuilles sont serrées à gauche, et possédant la propriété suivante : tout noeud de l’arbre a une valeur inférieure à celles de ses noeuds-fils.

Concrètement, voici un exemple de tas :

Les deux opérations à définir sur un tas sont :

• L’insertion d’un nouveau noeud lors de la création du tas
• L’extraction du noeud qui réalise le minimum pour la relation d’ordre

Toute la difficulté consiste à maintenir la structure de tas entre deux opérations.

Pour insérer un nouveau noeud, rien de plus simple, il suffit de l’ajouter tout en bas de l’arbre et de le faire remonter à sa place, c'est-à-dire à l’échanger avec son père tant que le poids de celui-ci (le père) est supérieur à son propre poids (le nouveau noeud). Cette opération porte généralement le joli nom de percolation. Au pire, on remonte le nouveau noeud jusqu'à la racine, donc l’algorithme correspondant tourne en O(ln n).

L’extraction paraît d’une simplicité déconcertante : il suffit d’extraire la racine du tas et le tour est joué. Le problème, c'est que le tas obtenu est tout sauf un tas, puisqu'il n’a même plus de racine… Une première solution consiste à faire "descendre le trou", en l’échangeant avec le plus petit de ses deux fils et en réitérant la démarche ; mais le tas obtenu gardera bien la propriété d’ordre, mais ne sera plus forcément bien rempli comme le montre l’exemple suivant :

 

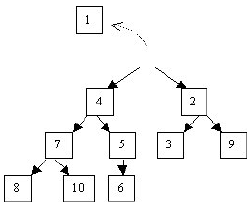
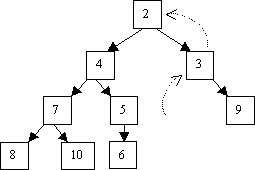
Une bonne solution est d’extraire la racine, de placer le dernier noeud du tas à sa place, et de faire descendre ce dernier jusqu'à sa place dans le tas. Sur l’exemple précédent, ceci donne :

  

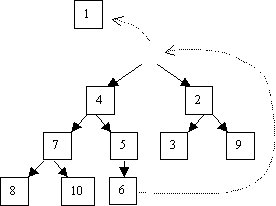
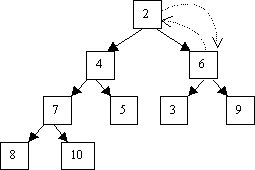
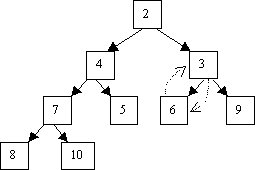
Comme pour l’insertion, on ne parcourt qu'une fois le tas, donc l’algorithme tourne en O(ln n).

Implémentation

L’aspect apparemment repoussant de la structure disparaît complètement à l’implémentation. En effet, un simple tableau suffit pour représenter un tas. Comme l’arbre est bien rempli, on vérifie sans aucun problème qu'en numérotant les noeuds de gauche à droite et de haut en bas, si i est le numéro d’un noeud, alors (i-1)/2 (division entière) est son père et, sous réserve que ses nombres ne dépassent pas la taille du tas, 2i+1 et 2i+2 ses fils. Moyennant cette remarque, le parcours d’un tas se fait quasiment les yeux fermés !

Oui, mais voilà…

En fait, dans l’implémentation suivante, les tas sont des objets un peu plus "gros". En effet, la relation d’ordre utilisée dans l’algorithme de Dijkstra repose sur un tableau qui varie à chaque étape de l’algorithme, tableau qu'il faut donc bien passer en argument quelque part lors de la création du tas… Ceci ne nuit en rien à la généralité de la définition, il suffit de passer NULL en argument pour obtenir un tas "normal". Mais ce n’est pas tout. Afin de pouvoir redonner au tas sa structure de tas lorsque la relation d’ordre sera modifiée, il faut connaître l’emplacement dans le tas d’un sommet i. D’où la nécessité de rajouter si besoin est (à l’aide d’un drapeau : "vrai" ou "faux", "faux" par défaut) un autre tableau inverse tel que inverse[i] soit la place de i dans le tas. (Pour le détail de chaque fonction, se reporter en Annexe).

   

   class Tas
   
   {
   
   int taille ; // taille courante du tas 
   
   int taille_max ; // taille maximale du tas (déterminée par celle de
   tableau)
   
   int * tableau ; // emmagasine les données du tas
   
   int * eval ; // Ce tableau sert à l’éventuelle évaluation des données du tas si celles-ci le nécessitent
   
   int * inverse ; // Ce tableau permet de retrouver l’indice d’un  élément de tableau, si celui-ci est inversible (flag=vrai et tableau[i]) 
   
   Bool flag ; // Booléen qui décide si l’on doit implémenter la fonction d’inversion du tableau
   
   fptr compare; // pointeur vers une fonction de comparaison des éléments du tableau
   
   Bool comparaison(int i, int j) ; // fonction de comparaison à proprement parler (utile dans le cas de l’implémentation du tableau eval) 
   
   void echange( int i, int j) ; // echange tableau[i] et tableau[j]    
   void descend(int i) ; // descend l’élément i dans le tas
   
   void remonte(int i) ; // remonte l’élément i dans le tas 
   
   public :
   
   //Constructeur 
   
   Tas (int n) ;
   
   Tas(int * ptr=NULL, int n=0, fptr comp=NULL, int * ptr2=NULL, Bool f =
   faux) ;
   
   // ptr : pointeur sur ce qui sera Tableau ; n : taille du tas ; comp : fonction de comparaison des entiers ; ptr2 : tableau auxiliaire qui sera eval ; f sera flag 
   
   // Destructeur
   
   ~Tas () ;
   
   // Méthodes externes 
   
   void SetTaille(int offset) ; // Permet d’"augmenter" la taille courante de 'offset'
   
   int GetTaille() ; // Renvoie la taille courante du tas
   
   int ExtrMinimum(); // Extrait le minimum (la racine) du tas, en lui conservant ses caractéristiques de tas 
   
   void Percolation(int i); // "percole" l’élément i (<=> remonte(i)) 
   
   int Inverse(int i) ; // renvoie k / tableau[k]=i si tas inversible (flag = vrai)
   
   void Tri() ; // tri le tas
   
   } ;