Implémentation de l’algorithme de Dijkstra
Implémentation de l’algorithme de Dijkstra
Résultat renvoyé par l’algorithme
Comme nous l’avons expliqué dans la partie précédente, l’algorithme de Dijkstra renvoie deux tableaux : distances et parcours. D’où la nécessité de créer une structure appropriée en C++ :
struct Res {
int taille ; // taille du graphe calculé
Sommet source ; // source des chemins considérés
int * distances ; // distances[i] est la distance totale de la source à i
int * parcours ; // parcours[i] est le sommet précédent i dans le parcours de la source à i
Res() ; // constructeur par défaut
~Res() ; // destructeur
void Affiche(FILE * f = stdout) ; // Affiche le résultat (sue l’écran ou dans un fichier)
} ;
L’algorithme en lui-même
Pas de remarque particulière à faire sur l’implémentation de l’algorithme de Dijkstra en lui-même. Elle ne fait que suivre les étapes précédemment mentionnées en s'appuyant sur les structures de données présentées… Là est tout le secret !
Res * Graphe::Djikstra(int source)
{
Res * resultat = new Res ;
int * distances = new
int [taille] ;
Sommet * parcours = new int [taille] ;
Sommet * C = new int [taille-1] ;
MatriceDouble * m =matricialisation() ;
for (int k=0 ; k<taille ; k++)
{
distances[k]=m->rep[source][k] ;
parcours[k]=source ;
}
// Initialisation de C
for (Sommet i=0, j=0 ; i<taille ; i++)
{
if (i!=source)
{
C[j]=i ;
j++ ;
}
}
Tas * T = new Tas(C, taille-1, (fptr) inf_str, distances, vrai) ;
T->Tri() ;
for (i=0 ; i<taille -2; i++)
{
Sommet mini = T->ExtrMinimum() ;
for (Rayons * l = m->adresse[mini]->sommet.liste ; l!=NULL ; l=l->suivant)
{
Sommet s = l->fleche.extrem ;
if (inf_str(somme(m->rep[mini][s] , distances[mini]),distances[s]))
{
distances[s]=somme(m->rep[mini][s] , distances[mini]) ;
parcours[s] = mini ;
T->Percolation (T->Inverse(s)) ;
}
}
}
delete m ;
delete T ;
delete [] C ;
resultat->distances = distances ;
resultat->parcours = parcours ;
resultat->taille = taille ;
resultat->source = source ;
return resultat ;
}
Petite interface
Qu'attendons-nous pour tester l’algorithme sur quelques graphes de notre cru ? Une petite interface conviviale ? Qu'à cela ne tienne, définissons un objet menu :
class Menu
{
char * nom ; // Titre du menu
int taille ; // Nombre d’options proposé
char * * composants ; // Tableau contenant le nom des options proposées
char * acces ; // tableau contenant les lettres qui permettent de choisir une option donnée
static int est_dans(char, char *) ; // teste si char est dans char * et renvoie sa position dans char * s'il existe
public :
Menu(char *, int, char * *, char *) ; // Constructeur paramétré (nom, taille, tableau de composantes, table d’accès)
~Menu() ; // destructeur
void Affiche() ; // Affichage du menu
int Reponse () ; // Attente de la réponse
} ;
Dans notre cas, le menu proposé est le suivant :
*** Menu principal *** [G] : creation interactive d’un Graphe [A] : Afficher un graphe [C] : Charger un graphe en format texte [S] : Sauver un graphe en format texte [T] : Trouver les plus courts chemins [E] : Enregistrer le resultat [Q] : Quitter Votre choix ?
La création interactive d’un graphe se comprend sans problème ; il faut juste décider au départ si on souhaite obtenir un graphe symétrique ou non (i.e. "des routes avec ou sans sens interdit"). Trouver les plus courts chemins lance bien entendu l’algorithme de Dijkstra une fois le sommet source précisé. Pour des raisons de commodité de programmation lors de l’appel récursif nécessaire pour trouver un chemin le plus court à proprement parler, les chemins les plus courts sont affichés dans l’ordre inverse, c'est-à-dire qu'il faut simplement les lire de droite à gauche…Il reste à dire un mot sur les formats de fichiers utilisés pour représenter les graphes… Se reporter à la partie suivante pour quelques exemples concrets :
Taille : n
Sommet : n
Extremite : i
Poids : pi
…
Extremite : j
Poids : pj
…
Sommet : n-1
…
…
Sommet : 0
…
Extremite : k
Poids : pk
L’ordre des sommets, tout comme l’ordre des arêtes, importe peu pourvu que les sommets apparaissent tous une et une seule fois (le programme de lecture commence par lire la taille du graphe et recherche alors les n sommets correspondants).
Deux petits exemples
Reprenons l’exemple du graphe S={d,a,o,u,s,t} , en renumérotant les sommets de 0 à 5 et en supprimant l’arête (d,d) (le plus court chemin de d à lui-même est nécessairement 0). Certes, ce graphe n’est pas connexe, mais tant qu'on ne s'occupe pas des chemins qui n’existent pas, l’algorithme fonctionne à merveille…
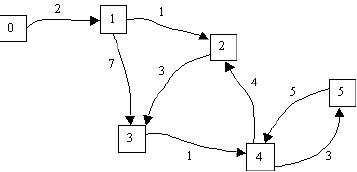
Taille : 6 Sommet : 5 Extremite : 4 Poids : 5 Sommet : 4 Extremite : 5 Poids : 3 Extremite : 2 Poids : 4 Sommet : 3 Extremite : 4 Poids : 1 Sommet : 2 Extremite : 3 Poids : 3 Sommet : 1 Extremite : 3 Poids : 7 Extremite : 2 Poids : 1 Sommet : 0 Extremite : 1 Poids : 2
Lançons Dijkstra sur le sommet 0 :
Source : 0 Parcours a l’envers de 0 a 1 : 1 0 Distance : 2 Parcours a l’envers de 0 a 2 : 2 1 0 Distance : 3 Parcours a l’envers de 0 a 3 : 3 2 1 0 Distance : 6 Parcours a l’envers de 0 a 4 : 4 3 2 1 0 Distance : 7 Parcours a l’envers de 0 a 5 : 5 4 3 2 1 0 Distance : 10
Pour les amateurs, un graphe un peu plus gros, et connexe cette fois :
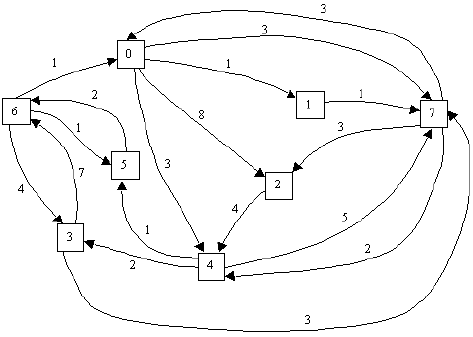
Taille : 8 Sommet : 7 Extremite : 4 Poids : 2 Extremite : 2 Poids : 3 Extremite : 0 Poids : 3 Sommet : 6 Extremite : 5 Poids : 1 Extremite : 3 Poids : 4 Extremite : 0 Poids : 1 Sommet : 5 Extremite : 6 Poids : 2 Sommet : 4 Extremite : 7 Poids : 5 Extremite : 5 Poids : 1 Extremite : 3 Poids : 2 Sommet : 3 Extremite : 6 Poids : 7 Extremite : 7 Poids : 3 Sommet : 2 Extremite : 4 Poids : 4 Sommet : 1 Extremite : 7 Poids : 1 Sommet : 0 Extremite : 7 Poids : 3 Extremite : 4 Poids : 3 Extremite : 2 Poids : 8 Extremite : 1 Poids : 1
C'est parti pour un petit Dijkstra appliqué au sommet 6…
Source : 6 Parcours a l’envers de 6 a 0 : 0 6 Distance : 1 Parcours a l’envers de 6 a 1 : 1 0 6 Distance : 2 Parcours a l’envers de 6 a 2 : 2 7 1 0 6 Distance : 6 Parcours a l’envers de 6 a 3 : 3 6 Distance : 4 Parcours a l’envers de 6 a 4 : 4 0 6 Distance : 4 Parcours a l’envers de 6 a 5 : 5 6 Distance : 1 Parcours a l’envers de 6 a 7 : 7 1 0 6 Distance : 3