Une solution ’trop’ simple : l’algorithme de Floyd

Il est difficile de parler d’algorithme naïf lorsqu'on s'attaque au problème des plus courts chemins, car quoi qu'il arrive, il faudra trouver un moyen de comparer différents chemins entre eux, de ne pas en oublier, bref de définir une façon de parcourir le graphe, ce qui, même à la main, est loin d’être instinctif. Malgré tout, l’algorithme de Floyd est l’un des plus simples à mettre en oeuvre… mais évidemment pas le moins coûteux, sinon à quoi bon se compliquer la vie avec l’algorithme de Dijkstra ?

Remarques préliminaires

Avant tout calcul, il faut d’abord s'assurer qu'un chemin le plus court existe bien entre les deux sommets considérés. Par la suite, on supposera donc que les graphes traités sont :

• connexes, ceci afin d’assurer l’existence d’un chemin allant de a à b
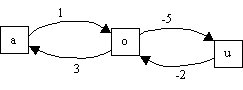• valués positivement, sinon l’existence d’un chemin le plus court n’est pas assuré. Ainsi, dans l’exemple suivant, il n’existe pas de chemin le plus court entre a et o

Description de l’algorithme

L’algorithme repose sur la remarque suivante : si (a₀,…,a_i,…,a_p) est un plus court chemin de a₀ à a_p , alors (a₀,…,a_i) est un plus court chemin de a₀ à a_i , et (a_i,…,a_p) un plus court chemin de a_i à a_p . De plus, comme les arêtes sont valuées positivement, tout chemin contenant un cycle est nécessairement plus long que le même chemin sans le cycle, si bien qu'on peut se limiter à la recherche de plus courts chemins passant par des sommets deux à deux distincts.

Floyd montre donc qu'il suffit de calculer la suite de matrices définies par : M_i,j^(k)=min(M_i,j^(k-1),M_i,k^(k-1) + M_k,j^(k-1))

En effet, une récurrence montre sans difficulté que pour k>0 , M_i,j^(k) est égal à la longueur du plus court chemin entre i et j, en ne considérant que les sommets intermédiaires 0,1,…,k . Ainsi, après n calculs, on obtient la matrice des longueurs des plus courts chemins.

Chaque matrice se calculant en O(n²) , l’algorithme final est en O(n³) . On verra par la suite que la solution de Dijkstra permet, pour le même résultat, un calcul en O(a²ln n) , justifiant par la même une complexité plus grande au premier abord.

En outre, si l’algorithme de Floyd a l’immense mérite de fournir tous les poids des chemins les plus courts, il reste que pour déterminer les chemins en question, il faut maintenir au fur et à mesure des calculs une autre matrice contenant en position (i,j) le sommet k par lequel il faut passer dans un chemin le plus court de i à j. Ensuite, par appel récursif, on peut remonter jusqu'au chemin proprement dit… gymnastique supplémentaire qui n’arrange rien au coût de l’algorithme…